PHAROS

Globalisation is driving a vast increase in international trade. Consequently, the industrial and commercial centres of the world become more interconnected with each other. This puts an enormous pressure on harbours, which play an essential role in the transport of goods. Harbours therefore increase their throughput capacity to cope with the demand. Besides these developments, local harbours also expand to provide space for an increasing fleet of leisure ships.

Depending on the function of the harbour, it will need to comply with safety and operational requirements. The design of the harbour needs to be such that hydraulic conditions are reduced and downtime of the quays is minimised. As construction works are expensive, it pays off to investigate the effectiveness (in reducing hydraulic loads) of the harbour design before construction.

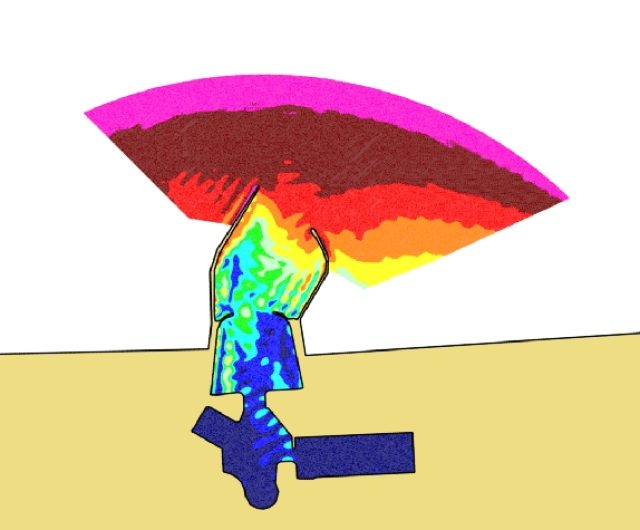
PHAROS study areas

Some typical study areas in which PHAROS is employed are:

• Assessment of the quality of a berthing location, in terms of safety or comfort,
• Comparison of mitigating measures such as different breakwater layouts or alternative quay wall designs,
• Determination whether and for which wave conditions a harbour basin will show resonant behaviour (seiching).

The latest PHAROS release (9.13.0.1 January 2019) introduces the possibility for expert-users to pre- and post-process runs in batch modus without the use of the GUI. This makes running a large number of runs more user-friendly.

Technical specifications

One of the most important aspects of harbour design is the extent to which both long and short waves penetrate to the berthing facilities. Moored ships may respond to these waves leading to downtime in loading and unloading operations or even to damage to mooring lines or fenders. Resonant harbour response to long waves can be particularly onerous, since moored large ships may have a corresponding resonant response.

The numerical wave model PHAROS (Program for HARbour Oscillations) accurately predicts the short wave penetration around coastal structures such as breakwaters and the resonant behaviour of enclosed areas to incident long waves. It therefore provides harbour developers with valuable information in the design phase of a harbour, or when harbour optimization is required.

Some typical study areas in which PHAROS is employed are:

• Assessment of the quality of a berthing location, in terms of safety or comfort,
• Comparison of mitigating measures such as different breakwater layouts or alternative quay wall designs,
• Determination whether and for which wave conditions a harbour basin will show resonant behaviour (seiching).

Theoretical background

PHAROS calculates the solution of the elliptic mild-slope equation formulated by Berkhoff (1972). This equation governs linear wave propagation over a mildly sloping bathymetry, with no restrictions to the water depth. The following physical processes are included:

• diffraction,
• refraction due to depth variations,
• refraction by ambient currents,
• shoaling

Directional and frequency spreading

The effect of directional spreading (short-crested waves) and frequency energy spreading (a spectrum) can be accounted for by combining the output of multiple computations. PHAROS includes routines that perform this operation, given a user-defined directional spreading function and/or a frequency spectrum. In the combined solution, the non-linear effects of wave breaking and bottom friction are also taken into account.

Seiching

Special procedures are also available to carry out computations for a large number of long wave periods to study long-wave resonance and seiching of harbours.

Boundary conditions

The boundary condition for the incoming wave signal is implemented in such a way that waves can pass and move out of the model domain without the use of sponge layers. Moreover, the shape of the incoming model boundary does not have to be circular, thus reducing the outer model area and therefore computational time. Boundary conditions are available for partially reflective and transmissive model boundaries. These can be used to model beaches, quay walls and breakwaters (also including wave overtopping or transmission).

Model grid

PHAROS solves the mild-slope equation on a boundary fitted finite element grid, using either Gaussian elimination (for small problems) or the iterative BCG method (bi-conjugate gradient).

Application

PHAROS can be applied for every harbour layout imaginable, from simple to very complex. It combines high quality computations with relatively low computational costs, enabling harbour developers to assess the quality of various harbour layouts. The two main areas of application are short wave agitation and long wave resonance (seiching).

Short wave agitation

PHAROS is mostly used to assess wave agitation in harbours. Once the basic grid has been prepared, changes in the geometry (for example the extension of a breakwater), bathymetry or reflection properties are easily implemented.

By repeating simulations for the modified layout, the effects of these changes on the wave heights in the harbour can be evaluated rapidly. In this way, the design of the harbour can be optimised, for example by estimating the consequences for the downtime at the berths.

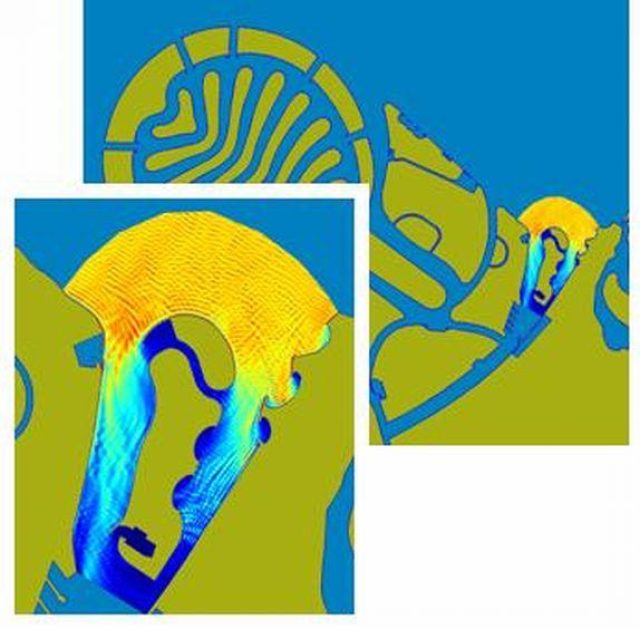
Long wave resonance

Another important application of PHAROS is harbour resonance (seiching) studies. In several harbours around the world, long waves are known to be a cause for problems either in the form of excessive motions of moored ships in apparently calm wave conditions. T

his occasionally leads to breaking of mooring lines, or strong oscillating flows in the harbour entrance. Long wave energy outside the harbour due to e.g. wave grouping, can be amplified for certain frequencies by the geometry of the harbour basin.

The seiching module of PHAROS allows to determine possible resonance of long waves in the harbour for a range of frequencies. This enables the user to determine the relevant wave periods for resonance and seiching. By evaluating the amplification of the wave height or the water velocity at critical positions in the port, possible risks for moored ships can be determined and possible mitigating measures evaluated.

Model organisation

Setting up a PHAROS model is straightforward and the process is well explained and documented in the extensive user’s manual. The following modules are used in the process of setting up a model, running it and visualizing the results:

• the user interface for input preparation and general control,
• the graphical grid editor to prepare the boundary fitted finite element grid,
• computational modules for long or short crested waves (with or without frequency spreading) as well as a module for seiching,
• visualization package Delft3D-QUICKPLOT.

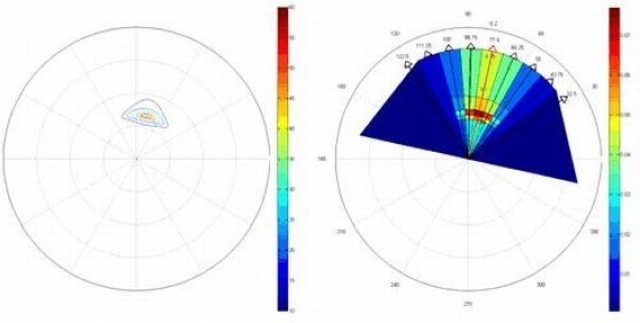
The PHAROS user interface is the starting point for all steps in the modelling process. It opens windows to prepare input, start the other modules as appropriate and provides support for case management. For directional and frequency spreading computations, visualization tools are available to check the schematization (discrete directions and periods) against the actual, user defined energy spectrum.

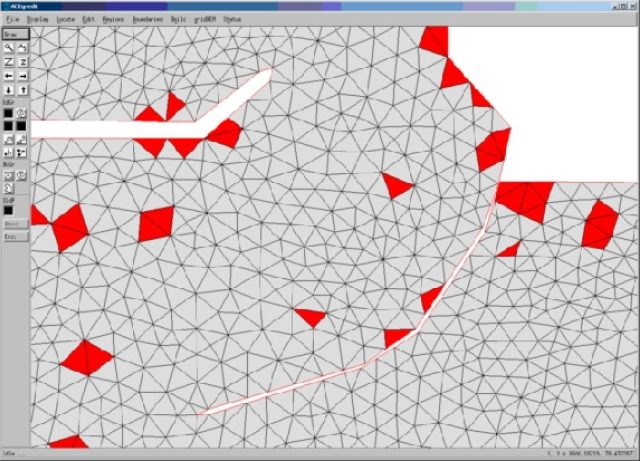
The graphical grid generator automatically generates the finite element grid, using the contour of the area to be modelled and a file containing depth values in that area. The dimensions of the cells will vary in size according to the local depth to obtain an optimal resolution of the grid. All sorts of options are available to check the quality and consistency of the grid and to modify the grid manually.

PHAROS has four modules to carry out the actual computations: one for a single, long crested run, one for simulations including directional spreading, one for simulations including directional and frequency spreading, and one for harbour resonance computations.

All four computational modules can be started directly from the user-interface, but they can also be run using script files (batch processing). This allows preparation of the required input for a number of simulations and execution of the runs when convenient.

For the presentation and analysis of the computation results, the program Delft3D-QUICKPLOT is coupled to PHAROS. This is a Matlab-based package, with many possibilities to visualize PHAROS results and other parameters such as the model bathymetry. In addition, figures can be saved and customized using Matlab, if necessary.

The PHAROS model software also contains a unique tool to process wave directions from the wave output fields of PHAROS computations. It can, for example, be used to identify incoming and outgoing wave components. The tool is based on a state-of-art technique called rotating DPRA. See De Jong & Borsboom (2012) and Janssen et al. (2001).

References

Battjes, J.A., and J.P.F.M. Janssen, 1978. Energy loss and set-up due to breaking random waves . Proc. 16th Int. Conf. Coastal Engineering, pp. 569-587.

Berkhoff, J.C.W., 1972. Computation of combined refraction-diffraction. Proc. 13st Int. Conf. on Coastal Engineering, Vancouver. ASCE, New York, pp. 471-490.

Borsboom, M.J.A. and M.P.C. de Jong, December 2012. A practical post-processing method to obtain wave parameters from phase-resolving wave model results. International Journal of Ocean and Climate Systems Volume 3, Number 4: 203–216. Multi-Science Publishing ISSN 1759-3131.

Hurdle, D.P., J.K. Kostense and P. van den Bosch, 1989. Mild-slope model for the wave behaviour in and around harbours and coastal structures in areas of variable depth and flow conditions. In: Advanced in water modeling and measurement.

Janssen, T.T., A.R. van Dongeren and C. Kuijper, 2001. Phase Resolving Analysis of Multidirectional Wave Measurements. Proc. Waves 2001 pages 377–386. San Francisco, CA, U.S.A.

Kostense, J.K., K.L. Meijer, M.W. Dingemans, A.E. Mynett and P. van den Bosch, 1986. Wave energy dissipation in arbitrarily shaped harbours of variable depth. Proc. 20st Int. Conf. on Coastal Engineering, Taipei. ASCE, New York, pp. 2002-2016.

Kostense, J.K., M.W. Dingemans and P. van den Bosch, 1988. Wave-current interactions in harbours. Proc. 21 st Int. Conf. on Coastal Engineering, Malaga. ASCE, New York.

Putnam, J.A. and J.W. Johnson, 1949. The dissipation of wave energy by bottom friction. Trans. Am. Geophysics Union, 30, 1, pp. 67-74.